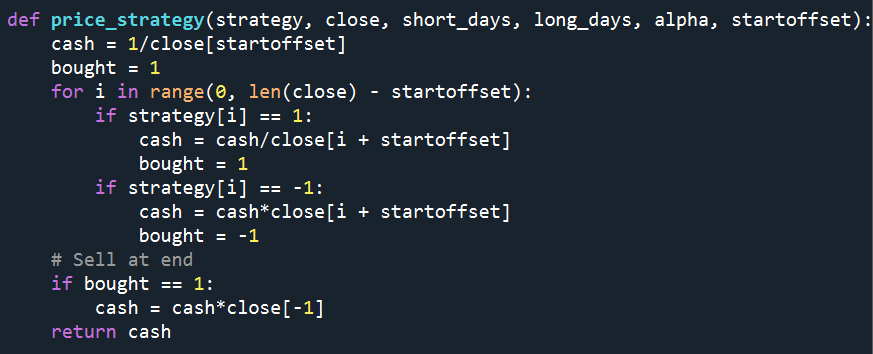
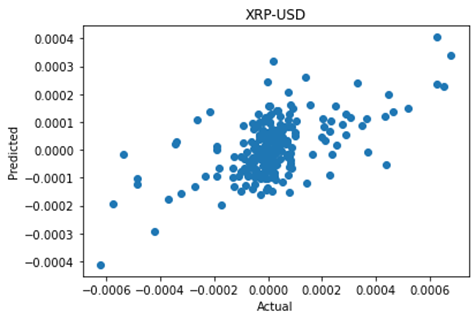
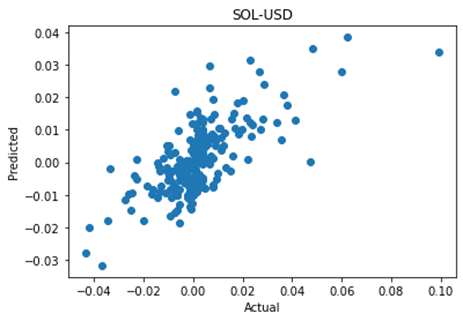
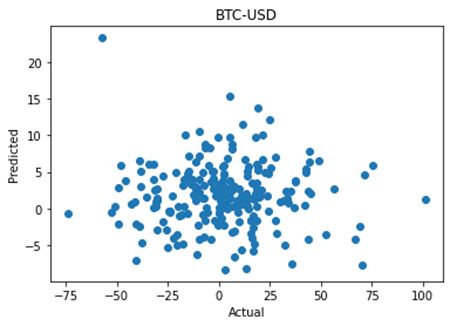
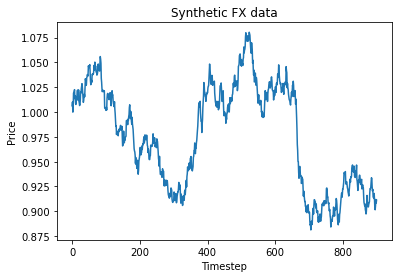
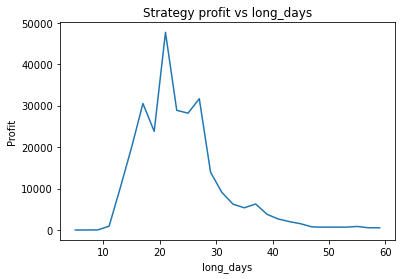
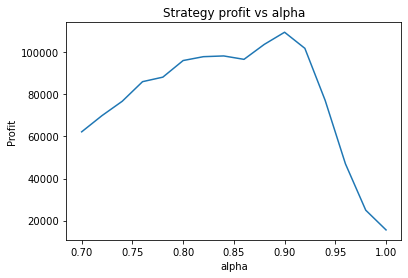
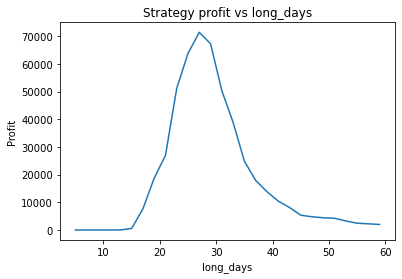
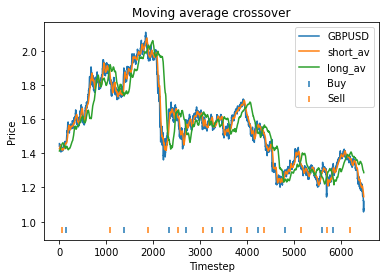
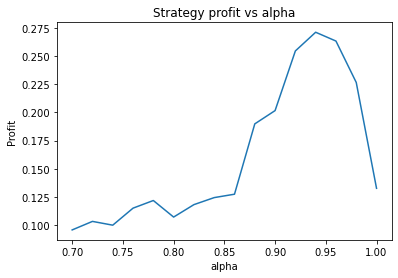
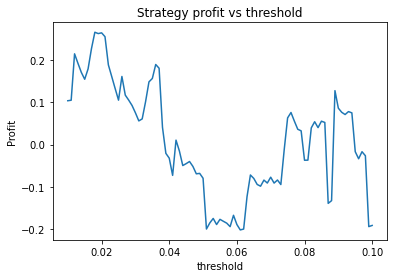
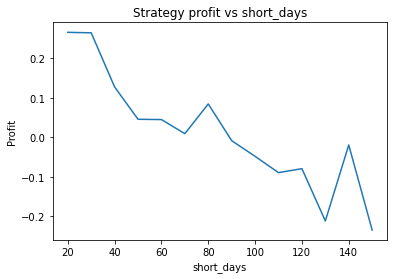
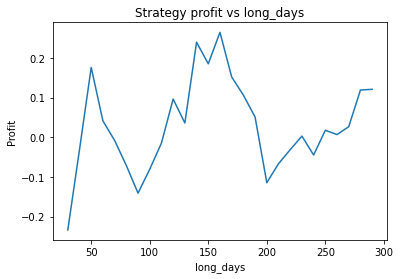
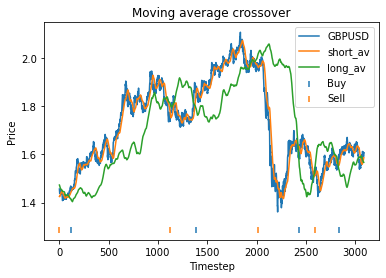
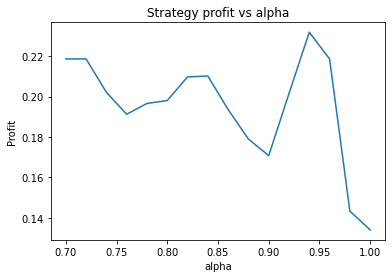
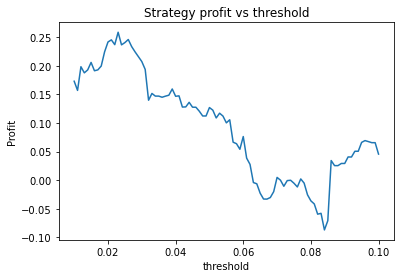
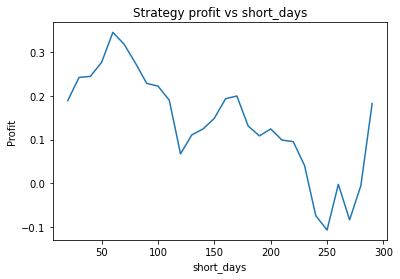
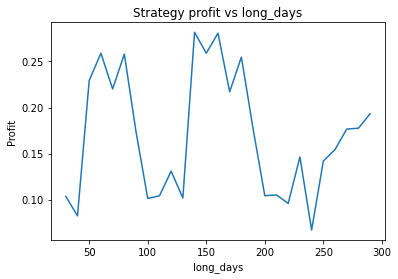
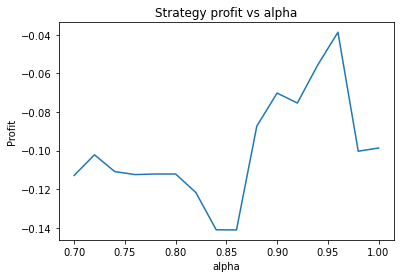
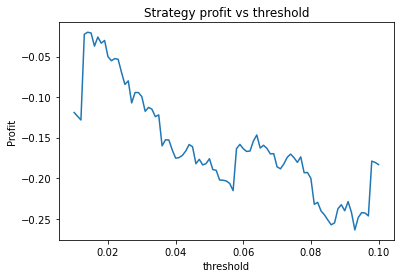
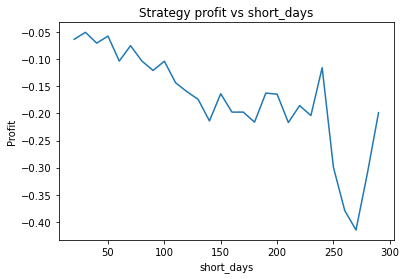
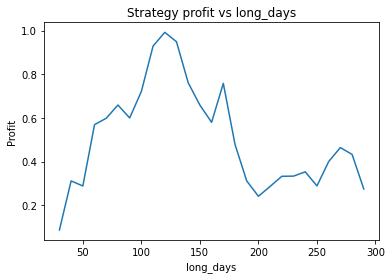
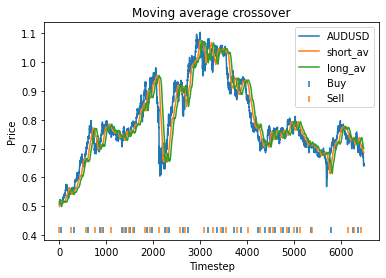
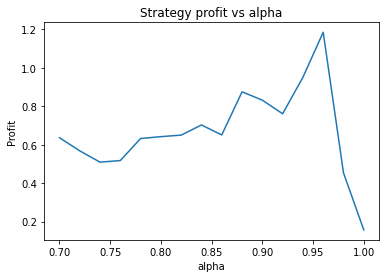
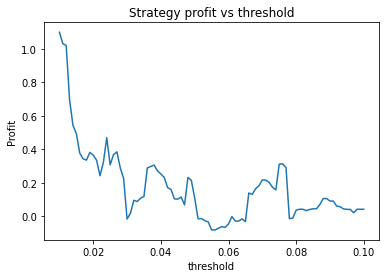
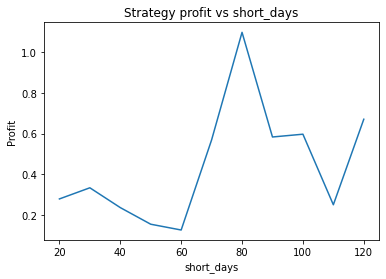
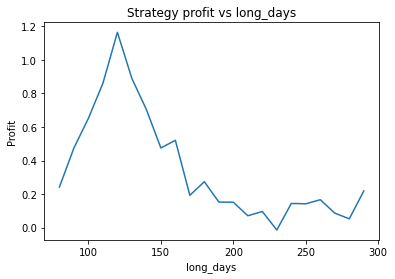
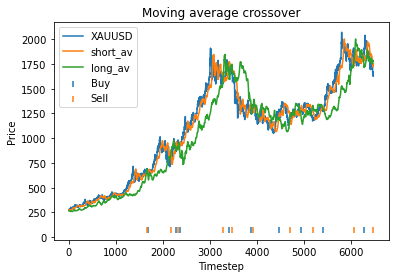
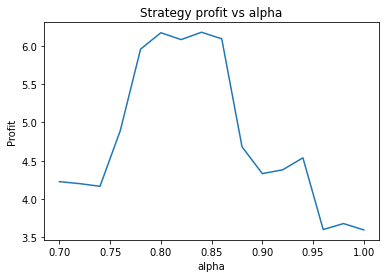
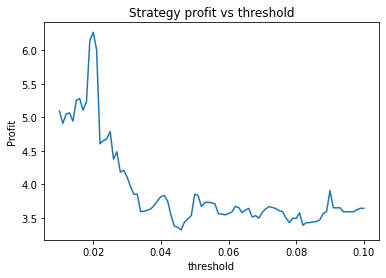
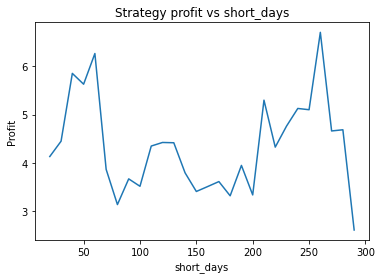
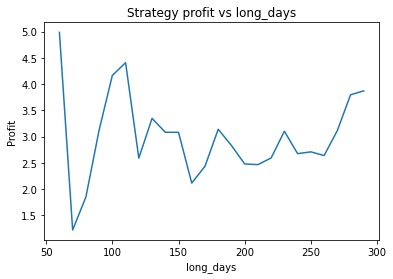
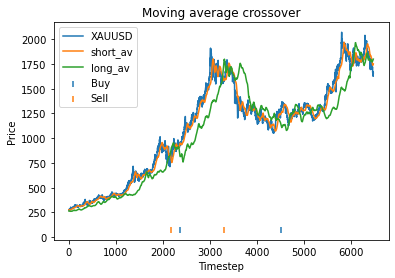
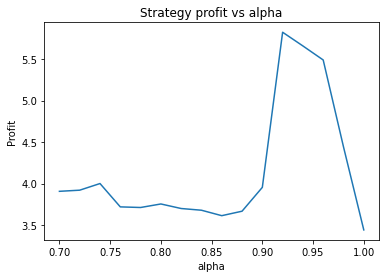
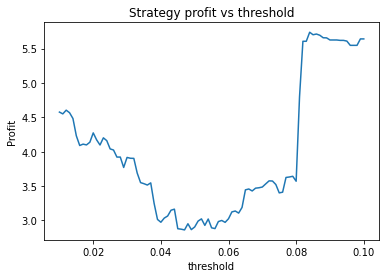
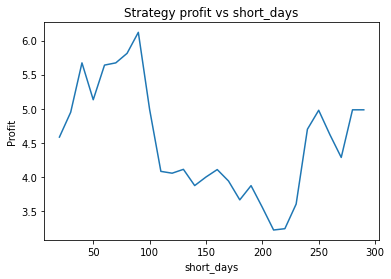
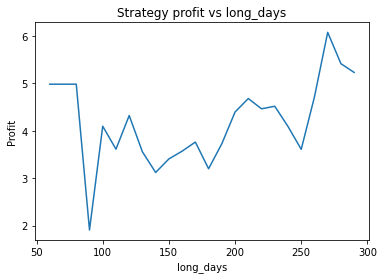
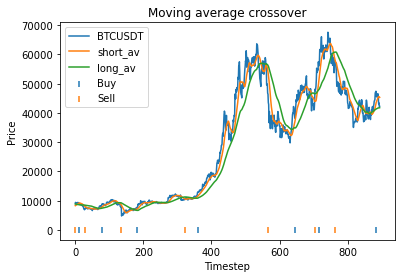
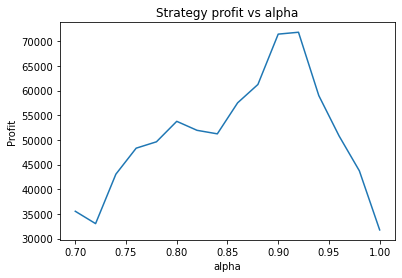
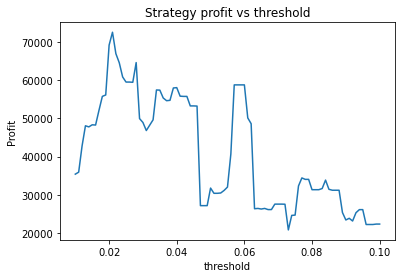
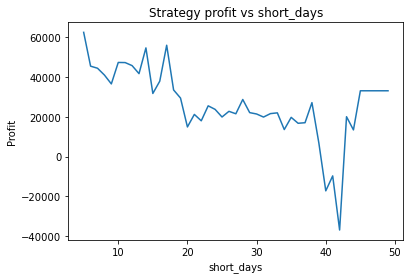
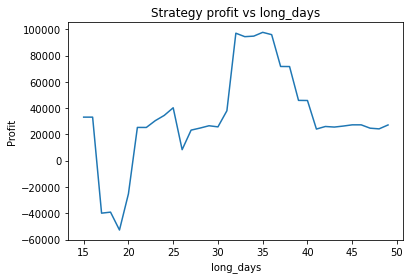
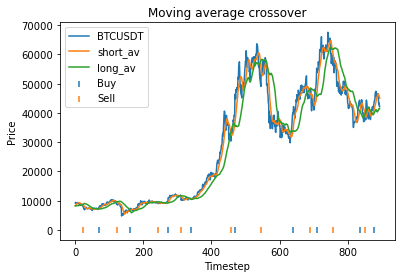
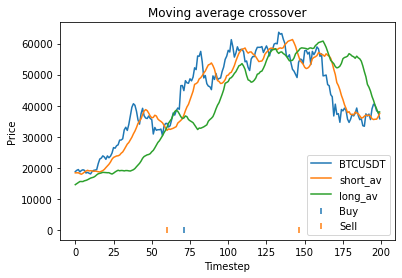
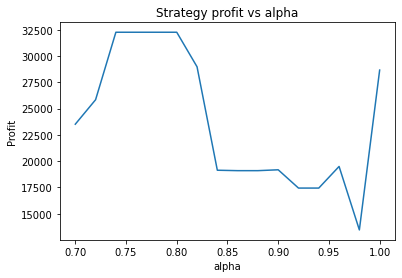
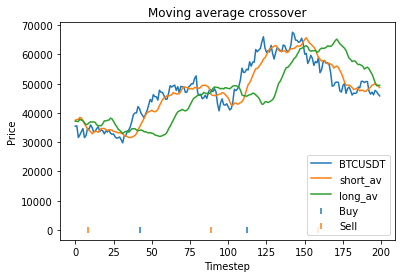
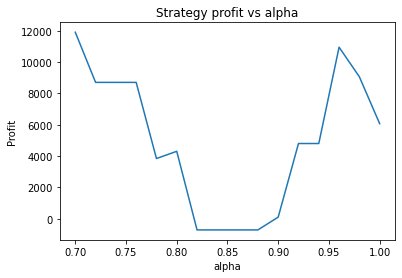
This is some code I wrote to generate a volatility surface in C++ using options and futures data, and use it to calculate price and Greeks for an ATM option. To simulate live trading, the code updates the volatility surface and option price as new data becomes available.
Note that the code is currently configured to execute for the first 150,000 lines of market data. This can be changed on by altering max_remaining_lines on line 62
Simplifications
Currently, the code creates only a single volatility smile for a single maturity. Of course, the code can quickly be adapted to generate a whole volatility surface, as this is just a number of smiles at different expiries with a suitable method of interpolating between them.
I used the future as a proxy for the forward, just based on the data I had. This is not strictly correct, as they can differ by a convexity correction. Also, rather than incorporate interest rate data, interest rates are currently assumed to be zero. Since the expiry used was short, this was acceptable.
Calculating Implied Volatilities
Implied volatilities are calculated using Newton’s method.
I’ve found that Newton’s method can fail to converge when converting volatility pillars from moneyness to delta, particularly for problematic vol surface data such as data containing arbitrage. However, these issues may not arise for a single implied volatility calculation. But convergence guarantees, and appropriate behaviour for all input data, should be further investigated for live trading code.
It’s also worth checking out our article on removing arbitrage from volatility surfaces.
Volatility Surface Construction
I took ATM to be the strike equal to the Futures value at expiry (that is, ATMF). Another possible convention is to use the strike for which a call and put have a delta of the same absolute magnitude.
For simplicity, I adopted the sticky strike convention to avoid having to convert volatility surfaces to delta. That is, the pillars of the vol surface are fixed strikes. I also adopted the common market convention of parameterising the vol surface using calls for strikes above ATM, and puts for strikes below ATM.
While cubic spline is market standard, this would have required either using a third party library or implementing it manually. Given my time requirements for this project, I chose linear interpolation between strike pillars. Flat extrapolation was chosen before the first and after the last pillar.
Volatility interpolation will not proceed if one of the two required pillar vols is missing. If the additional complexity was worthwhile, one could proceed to use the next pillar over if available. One could also attempt to use put in place of call (or vice versa) if the intended market price was not available. Note that the volatility surface output displays “-1” when volatility data is not yet available. As long as a valid volatility has been calculated at least once in the past, this will continue to be used. A possible modification would involve removing volatilities based on market prices that are either too old or no longer existing in the market.
Data Quality
The code uses the mid price if both bid and ask quantities are non-zero. If only one is non-zero, it will use that value. If both quantities are zero, the data is ignored and the volatility surface is not updated. That is, the row is interpreted as missing data.
Some data rows in the options input data seemed erroneous. In this case, Newton’s method could not find a volatility solution. I imposed a max_iterations of 100, and discarded such rows. Similarly, a volatility > 10 (1000%) was assumed to be due to erroneous data.
Greeks
The greeks delta, gamma, vega and theta are calculated using finite differences and a reasonable choice of step size. Although infinitesimal greeks are available via the Black-Scholes formula, traders may be more interested in the consequences of small, finite movements rather than infinitesimal movements. The greeks can be quite sensitive to the chosen step size.
Because I used Black’s formula for pricing which takes the forward as input, and spot data was not available, I outputed forward delta and forward gamma (that is, I shifted the forward value instead of the spot value). Delta will differ from spot by forward/spot and gamma by that amount squared. Theta is chosen to be a 1-day theta.
The decision was made to output updated option price and greeks whenever option call price changed by a tolerance of at least 0.00001. This condition could be modified depending on what exactly the reason is for outputting changed prices.
Code Structure
The primary auxillary functions are:
- “Black” to price calls and puts
- “Implied Vol” to use Newton’s method to calculate a volatility from a market price
- “PriceAndGreeks” to return a 5-vector price, delta, gamma, vega, theta.
- “InterpolateVol” to use linear interpolation and flat extrapolation to extract a volatility from the vol surface data.
- “UpdateVol” to update a volatility at a particular strike if either the corresponding market price has changed, or the forward has changed.
Presently, the remainder of the code, including file input/output and the primary loop through market data lines, occurs in the “main” function. Given more time, the main function could be broken down into multiple functions for cleaner, more reader and more reusable code (although the value of this depends on the ultimate purpose and future direction of the project).
Code Testing
The code begins with a few simple unit tests to test pricing, calculation of implied volatilities and volatility interpolation. Basic reasonableness examinations have been done on the output data, however more extensive testing should be done before putting such code into production.
C++ code
#include <iostream>
#include <fstream>
#include <vector>
#include <math.h>
#include <limits>
using namespace std;
vector<vector<string>> getData(string fileName, string delimiter);
vector<string> getDataSingleLine(string fileName, string delimiter);
void writeData(vector<vector<string>> Z, string fileName, string delimiter);
vector<string> split(const string& str, const string& delim);
double Black(double V, double F, double K, double T, double r, char callput);
double Ncdf(double x);
double ImpliedVol(double initialVolGuess, double targetPrice, double tol, double F, double K, double T, double r, char callput);
vector<double> PriceAndGreeks(double V, double F, double K, double T, double r, char callput);
double interpolateVol(double strike, double F, vector<double> CallStrikes, vector<double> CallVols, vector<double> PutVols);
void UpdateVol(int updated_symbol, double FuturePrice, double T, vector<double>& CallStrikes, vector<double>& CallVols, vector<double>& PutStrikes, vector<double>& PutVols, vector<double>& CallPrices, vector<double>& PutPrices);
int main()
{
// Unit tests
cout << "Unit tests" << '\n';
cout << "Call price should be 4.26894926: " << Black(0.1,100,99,1,0.05,'C') << '\n';
cout << "Call implied vol should be 0.1: " << ImpliedVol(0.05, 4.26894926, 0.00001, 100, 99, 1, 0.05, 'C') << '\n';
cout << "Put price should be 3.31771983: " << Black(0.1,100,99,1,0.05,'P') << '\n';
cout << "Put implied vol should be 0.1: " << ImpliedVol(0.15, 3.31771983, 0.00001, 100, 99, 1, 0.05, 'P') << '\n';
vector<double> teststrikes{1,2,3,4,5};
vector<double> test_vols_call{.10,.12,.14,.16,.18};
vector<double> test_vols_put{.102,.122,.142,.162,.182};
cout << "Interpolated vol should be .102: " << interpolateVol(0.9, 3, teststrikes, test_vols_call, test_vols_put) << '\n';
cout << "Interpolated vol should be .18: " << interpolateVol(5.1, 3, teststrikes, test_vols_call, test_vols_put) << '\n';
cout << "Interpolated vol should be .131: " << interpolateVol(2.5, 3, teststrikes, test_vols_call, test_vols_put) << '\n';
// Load data
string market_data_filename = "market_data.csv";
string static_info_filename = "static_info.csv";
// Output files
ofstream fittingfile("fitting_output.csv");
ofstream optionfile("option_output.csv");
// Format static data.
// This code assumes order of headings and that calls are labelled 1 to 145 and puts 146 to 290 with none missing.
// Code would need to be modified to handle more general input files or potential missing data.
vector<vector<string>> static_info = getData(static_info_filename, ",");
double expiry_time = stod(static_info[1][5]); // Assumes all options have the same expiry
vector<double> CallStrikes(145);
vector<double> PutStrikes(145);
for(int i = 1; i < static_info.size(); i++)
{
string symbol = static_info[i][0].substr(4, symbol.size() - 4);
if (static_info[i][3].compare("C") == 0) {CallStrikes[stoi(symbol)-1] = stod(static_info[i][4]);}
else if (static_info[i][3].compare("P") == 0) {PutStrikes[stoi(symbol)-146] = stod(static_info[i][4]);}
}
// Load market data
// To simulate the arrival of live trading data, data is loaded one line at a time, with volatility surface calculations updated every line.
ifstream file(market_data_filename);
int max_remaining_lines = 150000; // Used to run code for a limited number of rows only
string line = "";
double current_time;
int updated_symbol; // symbol that is updated this data row
double T; // time to expiry
getline(file, line); // First row are headings
// Most recent price update for each strike. -1 represents no data yet.
vector<double> CallPrices(145,-1);
vector<double> PutPrices(145,-1);
vector<double> CallVols(145,-1);
vector<double> PutVols(145,-1);
vector<double> OptionCallPrice(5,-1);
double FuturePrice = -1;
// Output files
vector<string> heading_row;
heading_row.push_back("Timestamp");
for(int i = 1; i < CallStrikes.size(); i++)
{
heading_row.push_back(to_string(CallStrikes[i])); // Assuming call strikes and put strikes are the same, which seems to be the case
}
for(int l = 0; l < heading_row.size(); l++)
{
fittingfile << heading_row[l] << ",";
}
fittingfile << "\n";
vector<string> heading_row2 {"Timestamp","Vol","Call price","Call delta","Call gamma","Call vega","Call theta","Put price","Put delta","Put gamma","Put vega","Put theta"};
for(int l = 0; l < heading_row2.size(); l++)
{
optionfile << heading_row2[l] << ",";
}
optionfile << "\n";
vector<vector<string>> pricing_output;
// Main loop. Reads each line in market data input and updates futures price, vol surface and option price/greeks where appropriate.
while (getline(file, line) && max_remaining_lines > 0)
{
vector<string> column = split(line, ",");
max_remaining_lines = max_remaining_lines - 1;
current_time = stod(column[1]);
T = (expiry_time - current_time)*pow(10,-9)/31536000; // convert nanoseconds to years
updated_symbol = stoi(column[0].substr(4, column[0].size() - 4));
// Code to find most appropriate price to use for current symbol
double current_bid = stod(column[2]);
int bid_quantity = stod(column[3]);
double current_ask = stod(column[4]);
int ask_quantity = stod(column[5]);
if (bid_quantity == 0 && ask_quantity == 0) {continue;} // Interpreted as no data update
if (current_bid == 0 && current_ask == 0) {continue;} // Interpreted as no data update
double mid = 0;
// if one has quantity zero, use the other
if (bid_quantity == 0 and ask_quantity > 0){mid = current_ask;}
else if (bid_quantity > 0 and ask_quantity == 0){mid = mid + current_bid;}
else {mid = (current_bid + current_ask)/2;}
// Update prices
if (updated_symbol == 0) {FuturePrice = mid;}
else if (updated_symbol <= 145)
{
CallPrices[updated_symbol-1] = mid;
}
else
{
PutPrices[updated_symbol-146] = mid;
}
// Update volatilities
if (FuturePrice < 0) {continue;} // unable to calculate volatilities without a forward
if (updated_symbol == 0) // If Future price has changed, all vols must be updated
{
for(int l = 1; l < CallVols.size()+ PutVols.size() + 1; l++)
{
UpdateVol(l, FuturePrice, T, CallStrikes, CallVols, PutStrikes, PutVols, CallPrices, PutPrices);
}
}
else{UpdateVol(updated_symbol, FuturePrice, T, CallStrikes, CallVols, PutStrikes, PutVols, CallPrices, PutPrices);}
// If V or F have changed, output ATM option price and greeks.
double impliedATMvol = interpolateVol(FuturePrice, FuturePrice, CallStrikes, CallVols, PutVols);
// If required vol pillars are still missing from vol surface data, no option price can be output
if (impliedATMvol > 0)
{
double oldprice = OptionCallPrice[0];
OptionCallPrice = PriceAndGreeks(impliedATMvol, FuturePrice, FuturePrice, T, 0, 'C');
if(abs(OptionCallPrice[0] - oldprice) > 0.00001) // only write a row to file if price has changed.
{
vector<double> OptionPutPrice = PriceAndGreeks(impliedATMvol, FuturePrice, FuturePrice, T, 0, 'P');
optionfile << to_string(current_time) << ",";
optionfile << to_string(impliedATMvol) << ",";
for(int l = 0; l < OptionCallPrice.size(); l++)
{
optionfile << to_string(OptionCallPrice[l]) << ",";
}
for(int l = 0; l < OptionPutPrice.size(); l++)
{
optionfile << to_string(OptionPutPrice[l]) << ",";
}
optionfile << "\n";
}
}
// Output fitting csv
// epoch nanoseconds, fitted volatility at each strike
vector<string> fitting_row;
fitting_row.push_back(to_string(current_time));
for(int i = 1; i < CallVols.size(); i++)
{
if (CallStrikes[i] < FuturePrice) {fitting_row.push_back(to_string(PutVols[i]));}
else {fitting_row.push_back(to_string(CallVols[i]));}
}
for(int l = 0; l < fitting_row.size(); l++)
{
fittingfile << fitting_row[l] << ",";
}
fittingfile << "\n";
}
file.close();
fittingfile.close();
optionfile.close();
return 0;
}
// Update the vol at a given strike
void UpdateVol(int updated_symbol, double FuturePrice, double T, vector<double>& CallStrikes, vector<double>& CallVols, vector<double>& PutStrikes, vector<double>& PutVols, vector<double>& CallPrices, vector<double>& PutPrices)
{
double tolerance = 0.0000001;
double r = 0; // Assumption of zero interest rates
double initialVolGuess;
if (updated_symbol <= 145)
{
if(CallPrices[updated_symbol-1] < 0) {return;}
double mid = CallPrices[updated_symbol-1];
if (CallVols[updated_symbol-1] < 0) {initialVolGuess = 0.15;}
else {initialVolGuess = CallVols[updated_symbol-1];}
double impvol = ImpliedVol(initialVolGuess, mid, tolerance, FuturePrice, CallStrikes[updated_symbol-1], T, 0, 'C');
if (impvol > 0 && impvol < 10)
{
CallVols[updated_symbol-1] = impvol; // ImpliedVol returns -1 if Newton fails to converge
}
}
else
{
if(PutPrices[updated_symbol-146] < 0) {return;}
double mid = PutPrices[updated_symbol-1];
if (PutVols[updated_symbol-146] < 0) {initialVolGuess = 0.15;}
else {initialVolGuess = PutVols[updated_symbol-146];}
double impvol = ImpliedVol(initialVolGuess, mid, tolerance, FuturePrice, PutStrikes[updated_symbol-146], T, 0, 'P');
if (impvol > 0 && impvol < 10)
{
PutVols[updated_symbol-146] = impvol;
}
}
}
// Linearly interpolate the vol smile for some strike
double interpolateVol(double strike, double F, vector<double> CallStrikes, vector<double> CallVols, vector<double> PutVols)
{
// Assume callstrike list is identical to putstrike list, and callstrike list is ordered
// Flat extrapolation
if (strike <= CallStrikes[0]) {return PutVols[0];}
if (strike >= CallStrikes[CallStrikes.size() - 1]) {return CallVols[CallVols.size() - 1];}
int rightindex = 0;
for(int i = 0; i < CallStrikes.size(); i++)
{
if (strike < CallStrikes[i]){rightindex = i; break;}
}
double right_strike = CallStrikes[rightindex];
double left_strike = CallStrikes[rightindex - 1];
double right_vol;
double left_vol;
// Use put for strike below ATM and call otherwise
if (left_strike < F) {left_vol = PutVols[rightindex - 1];}
else {left_vol = CallVols[rightindex - 1];}
// If vols don't exist yet return -1
if (left_vol < 0 or right_vol < 0) {return -1;}
if (right_strike < F) {right_vol = PutVols[rightindex];}
else {right_vol = CallVols[rightindex];}
return left_vol + (right_vol - left_vol)*(strike - left_strike)/(right_strike - left_strike);
}
vector<double> PriceAndGreeks(double V, double F, double K, double T, double r, char callput)
{
double deltastep = 0.0001*F;
double gammastep = 0.01*F;
double vegastep = 0.0001*V;
double thetastep = min(1.0/365,T);
vector<double> result(5,0);
double price = Black(V, F, K, T, r, callput);
result[0] = price;
result[1] = (Black(V, F + deltastep/2, K, T, r, callput) - Black(V, F - deltastep/2, K, T, r, callput))/(deltastep/2);
result[2] = (Black(V, F + gammastep, K, T, r, callput) + Black(V, F - gammastep, K, T, r, callput) - 2*price) / pow(gammastep, 2);
result[3] = (Black(V + vegastep/2, F, K, T, r, callput) - Black(V - vegastep/2, F, K, T, r, callput))/(vegastep/2);
result[4] = (Black(V, F, K, T - thetastep, r, callput) - price)/thetastep;
return result; // price, delta, gamma, vega, theta
}
// Uses Newton's method to calculate implied volatility from market price
double ImpliedVol(double initialVolGuess, double targetPrice, double tol, double F, double K, double T, double r, char callput)
{
double derivativeStep = min(0.00001, tol/100);
double currentVol = initialVolGuess;
double functionValue = Black(currentVol, F, K, T, r, callput) - targetPrice;
double derivativeValue;
int max_iterations = 100;
while (abs(functionValue) > tol){
derivativeValue = (Black(currentVol + derivativeStep, F, K, T, r, callput) - functionValue - targetPrice)/derivativeStep;
currentVol = currentVol - functionValue / derivativeValue;
functionValue = Black(currentVol, F, K, T, r, callput) - targetPrice;
max_iterations = max_iterations - 1;
if (max_iterations == 0) {return -1;}
}
return currentVol;
}
// Prices a put or call option using Black's formula and the forward value
double Black(double V, double F, double K, double T, double r, char callput)
{
constexpr double lowest_double = std::numeric_limits<double>::lowest();
if (T < lowest_double) {return F-K;} // avoid divide by 0
double d1 = (log(F/K) + pow(V,2)*T/2)/(V*sqrt(T));
double d2 = d1 - V*sqrt(T);
if (callput == 'C')
{
return exp(-r*T)*(F*Ncdf(d1)-K*(Ncdf(d2)));
}
else if (callput == 'P')
{
return exp(-r*T)*(-F*Ncdf(-d1)+K*(Ncdf(-d2)));
}
}
// Normal cumulative cdf function
double Ncdf(double x)
{
return erfc(-x / sqrt(2))/2.0;
}
void writeData(vector<vector<string>> Z, string fileName, string delimiter)
{
ofstream file(fileName);
for(int k = 0; k < Z.size(); k++)
{
for(int l = 0; l < Z[0].size()-1; l++)
{
file << Z[k][l] << delimiter;
}
file << Z[k][Z[0].size()-1] << "\n";
}
file.close();
}
vector<vector<string>> getData(string fileName, string delimiter)
{
ifstream file(fileName);
vector<vector<string> > Z;
string line = "";
while (getline(file, line))
{
vector<string> vec = split(line, delimiter);
Z.push_back(vec);
}
file.close();
return Z;
}
vector<string> getDataSingleLine(string fileName, string delimiter)
{
ifstream file(fileName);
vector<string> data;
string line = "";
getline(file, line);
data = split(line, delimiter);
file.close();
return data;
}
vector<string> split(const string& str, const string& delim)
{
vector<string> tokens;
size_t prev = 0, pos = 0;
do
{
pos = str.find(delim, prev);
if (pos == string::npos) pos = str.length();
string token = str.substr(prev, pos-prev);
tokens.push_back(token);
prev = pos + delim.length();
}
while (pos < str.length() && prev < str.length());
return tokens;
}