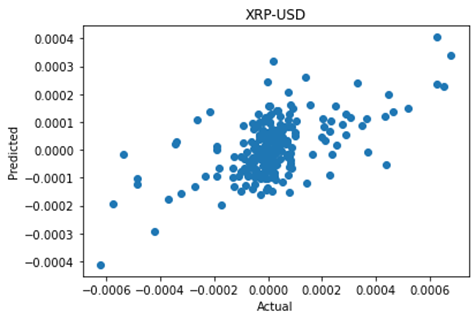
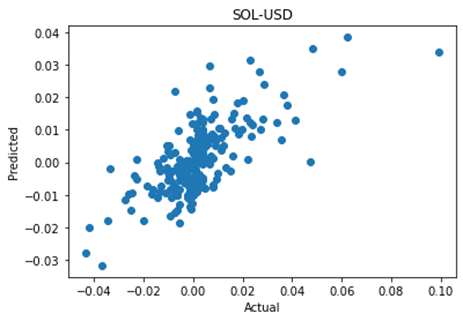
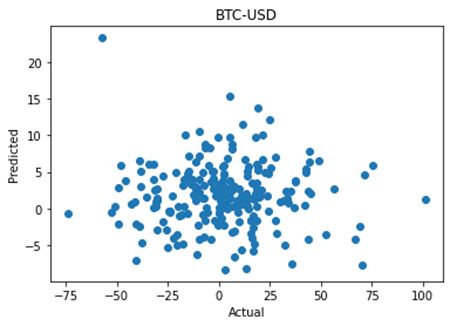
Hiring managers are put in the position of speculating on the future job performance of candidates. This is true whether they are looking to hire a permanent staff member, or engage a consultant or freelancer for a shorter time period or on a less than fulltime basis.
Yet, their field of expertise is in executing their own jobs, not in appraising the capabilities of another person. While hiring managers might receive interview training from their firm’s HR department, this merely shifts the burden of developing an effective candidate assessment process onto HR personnel. Anyone who has done one of those personality tests which ask you the same highly ambiguous questions over and over in slightly different ways, will know that the only people with no scepticism in the validity of this methodology are HR themselves.
While some of what I say may be applicable to other kinds of roles, I want to focus on hiring for quants (quantitative finance) and mathematicians. As a quant and mathematician myself, and having been through a few interviews myself during my career, and I’ve got a few opinions on this, so strap in!
Jim Simons, mathematician and founder of Renaissance Technologies, described how he chose the 150 PhDs working for him by saying he looked for people who had “done research and done it well”. In other words, he looked for people who had shown they could succeed at challenging projects, even though their previous work had nothing to do with the work they would be doing. This is pretty much the opposite of most hiring managers who ideally want to hire someone who has done as close as possible to the same job before. As the long term annual return of 62% of shows, it worked out pretty well for him.
So how do managers try to interview quants and mathematicians, and why doesn’t it work?
A difficult task under any circumstances
Judging other people is a difficult task at the best of times. Consider the following examples:
- J.K. Rowling was rejected by 12 publishers before she found success. Given that the Harry Potter franchise is now worth tens of billions, it’s safe to say that those publishers were not as good at picking the winners as they might have thought they were. Even though picking which authors will make them money is supposed to be the primary skill of a publishing house.
- Most elite trading firms (and even the less elite ones!) like to screen their candidates with online coding and maths tests, apparently believing that this will allow them to select the “smartest” people. And in the news, I occasionally see articles alleging that some kid has an IQ higher than Einstein. The implication being that this kid should go on produce achievements at least as great as Einstein’s. Yet, documentaries which have followed up on high-IQ children year later have found that they’ve become competent professionals, but not the singular individuals their singular IQ scores suggested they would. And Einstein struggled to find a teaching position after graduating, and instead spent 7 years working at a patent office – retrospectively, probably not the best use of his abilities. Why did not one person in society, including academics and professors, anticipate his potential? Couldn’t they have just sent him to do an online test like the Susquehannas, Citadels or Towers of the world? As a slow, deep thinker, I suspect Einstein would not have done unusually well on those kinds of tests.
- Rachmaninoff’s first symphony was savaged by critics, with one comparing it to the seven plagues of Egypt. Yet today he is one of the most enduringly popular romantic composers.
Google famously analysed how job performance aligned with interview performance:
“”We looked at tens of thousands of interviews, and everyone who had done the interviews and what they scored the candidate, and how that person ultimately performed in their job. We found zero relationship. It’s a complete random mess” He also admitted that brainteasers are useless and only good for making the interviewers feel smart.”
So why don’t interview questions work?
It’s important to remember that the purpose of an interview is to try to determine how a candidate will perform in the work environment. Therefore, the candidate should be observed under circumstances as close as possible to the work environment. Yet, the interview differs profoundly from the normal work environment in several critical ways:
The interviewer fails to understand how specific their questions are, and underestimates transferrable skills.
In my opinion, many managers, and perhaps the majority, make the mistake of disregarding general skills and abilities, and general candidate quality, in favour of very specific past experience.
A former manager of mine called it “looking for the person who was doing the job before”. Ideally, the manager is looking for the person who just quit that very role. Or, failing that, someone who has been doing almost exactly the same role at a competitor.
This is reflected in the interview by the asking of very specific questions. Since the number of topics in either mathematics or quantitative finance is almost unlimited, the candidate may well not have spent time on those very specific topics. Or, they may have done so many years ago but can no longer recall off the top of their head.
For example, if you were to ask me for the definition of a (mathematical) group, I would struggle to recall off the top of my head. Likewise if you were to ask me to write down the Cauchy Riemann equations. Although these are both first year university topics, I simply haven’t looked at them in quite a while. However, if I needed one of these during the course of my work day, I look it up, and seconds later I’m moving forward with my work. It’s very unwise to interview experienced professionals by testing whether they can recall first year university topics off the top of their heads under pressure. Yet, interviews for quants (as well as software developers) are often conducted in this way. And I’ll give some real world examples of this below.
I remember when I was doing Josh Waitzkin’s chess tutorials that come with the Chess Master computer program, he talked about how, after studying a huge number of chess games, he had forgotten all the specifics of those games. Yet, something remained. A kind of intuition or deep understanding that didn’t depend on remembering any particular specifics.
An interviewer can be very impressed with a candidate’s knowledge, or surprised that they don’t know anything, all based on the luck of whether they ask questions the candidate happened to have thought about fairly recently. Furthermore, since the interviewer chooses questions that they know well or have prepared, it can easily appear to them that they seem to know a lot more than any of the candidates that they interview. If the candidate were able to choose questions for the interviewer to answer, an identical dynamic may occur. Sometimes, the interviewer’s limited knowledge leads them to test candidates memory of elementary facts, while the candidates knowledge is much broader than they realise. Interview questions constitute a set of measure zero in the set of all knowledge in the field.
Another thing to keep in mind is that, just because someone has been doing a certain kind of role for many years, doesn’t necessarily mean they are good at it. There are many university lecturers who have been teaching for 30 years, and yet the students find their courses poorly structured and confusing. This means that hiring someone with past experience in the exact same role may not be preferable to choosing a high quality candidate with who’s work history is not exactly the same as the present role.
I’ve also found that some quants and software developers can have difficulty with seemingly mundane tasks like understanding and responding to emails, proofreading their reports, even though they may pass technical interview questions.
The candidate has no opportunity to prepare for the tasks.
In the workplace, people don’t come up to you and insist you produce a random fact off the top of your head in 10 seconds. Nor do they insist you engage in rapid problem solving challenges while they wait and glare at you.
When you are assigned a task in the workplace, you probably won’t instantly understand all aspects of it. It might require information you don’t yet know, or information you once knew but have forgotten because you haven’t needed to use it in your job for a few years. Either way, you use google, wikipedia, you look up some books, and soon you’re moving the task towards completion.
Usually when you start a new role, the first couple of months involve a period of learning. This is because, even though you may have many years of experience in similar roles, every firm and every role has it’s own set of specific financial products, calculational methodologies and coding tools.
Some people suggest “preparing” for interviews. This is both difficult and a waste of time, since you could spend time preparing information and find the interviewer asks you something completely different. It’s silly to try to know everything all at once. A reasonable person researches the specific facts they need for a task, when they need to. Indeed, researching a new problem or task which is not exactly the same as something you did before, is a very important skill, much more important that memorisation. And it’s a skill which is totally untested in an interview.
Now, universities also try to assess people – they do this using exams. But there is one key difference between the assessment of universities and the assessment of interviewers. When you are given an exam at university, you are first told what knowledge and skills you need to master, and afforded the opportunity to do so throughout the semester. Of course, you won’t know exactly which questions will be asked in the exam but, if the lecturer has done a good job, the exam questions should a subset of those you were made aware that you needed to learn to do. You are not being assessed on whether you know x or can do y off the top of your head in seconds. Rather you are being assessed on, if the need to know x or do y arises in your job, can you go away and learn x or learn to do y?
Studies have shown that interviews not only add nothing of value above just considering a candidate’s university marks, but can actually be worse than just judging candidates by their university marks (see this article in the New York Times). Why? Because university exams are an objective measure of whether a candidate is able to achieve a task assigned to them, given an appropriate amount of time to think, research and learn. Exactly like the workplace! Interviews, on the other hand, are not representative of either the university environment or the workplace environment.
When I was a university lecturer in mathematics, I watched some students struggle when transitioning from early undergraduate courses to more advanced courses. These students had perfected a learning strategy of memorizing how to do the specific kinds of problems they suspected were going to be on the exam. But in advanced courses, they were asked to creatively generate their own proofs that did not necessarily match a pattern of anything they had seen before. What was needed here was an approach of developing general skills and conceptual understanding, not memorising how to do certain very specific problems.
And as a mathematics or physics researcher, there is no point in memorising specific topics. Because you have no idea what knowledge or skills the next research project you undertake will require. Rather, the skillset you acquire is the ability to quickly look up and learn things, when you need to know them.
A prospective consulting client once presented to me a paper on quantitative finance that he had been reading, and asked me if I was “familiar with it”. When you consider that someone could spend their entire lives reading papers in a given discipline and still not be familiar with almost all of them, it’s unlikely this client will find a consultant who has coincidentally read the exact paper he’s been looking at. Another client was looking for an expert in “Markov chains”. Not an expert in mathematics with a PhD, who could apply their general skills to many different problems including Markov chains, but someone who specifically specialized in the exact topic the client was interested in. Just like the kinds of interviews I’ve been discussing, these clients were focused on very specific knowledge rather than the broad applicability of general capabilities.
As a very experienced classical pianist, I can provide a good analogy here. If an interviewer were to try to test my claim of being an experienced pianist by challenging me to play Fur Elise, I can tell you that I wouldn’t be able to do so very well. The reason is that, although this is an easy piece, I haven’t played it in ten or fifteen years. In fact, I may never have properly learnt this piece even as a student. Even though it is an easy piece, I still need time to prepare it and learn/relearn what the notes are. However, I can perform Rachmaninoff’s third piano concerto for the interviewer, one of the most challenging pieces written for piano, simply because I have prepared this piece. A pianist does not have the ability to play any piece, even an easy one, off the top of their heads. The skillset of a pianist is rather to go away and prepare and master a piece, when they are assigned the task of doing so. I believe the same is true of a mathematician or a quant.
The candidate is under a lot of pressure in an interview.
Finally, another key issue that interviewers need to be very aware of is that the interview may be testing how the candidate behaves when under a specific kind of pressure that doesn’t arise in the real workplace. Furthermore, when under pressure, memory may function but careful thinking may be difficult. This would again cause the interviewer to select people who have memorised certain facts, over people who can think about them and figure them out when they need them.
I’ve had interviewers ask me probability questions that 14 year olds would solve in their high school maths classes. It’s strange that an experienced quantitative professional would test another experienced quantitative professional with questions from early high school. This can only really be testing one of two things: 1) Can you remember how to solve, off the top of your head, a problem you haven’t thought about in 20 years? 2) Can we prove that when you’re nervous you might make a mistake on a simple problem? I believe that neither of these is a useful gauge of workplace performance.
Case studies
As case studies, I offer some of the interviews and discussions with clients that I myself have encountered!
Get them to do the work before deciding whether you want to pay them to do the work.
Occasionally I get clients who want to know, right off the bat, how I’ll solve the problem, what the outcome will be, and how long it will take. Needless to say, these questions cannot be answered at time t=0 of a research project. Rather, the first step is for the consultant to begin to read through the documents and papers provided by the client, and begin to build up an understanding of the project. Answers about which technical approach is appropriate, or whether the project is even possible, will begin to take shape over time. In fact, clarifying these questions may be most of the work of the project, rather than something that happens before the project begins.
It reminds me of academics who finish their research project, before applying for an academic grant to fund the now finished research. They then use this money to fund their next project instead. The idea is that, once the research is finished, you can show the grant board exactly what methods you plan to use, how long it will take you, and that you’re certain this approach will work. If you instead go to the grant board saying you’re going to “attempt” to solve the problem, using as yet unknown method, and have no idea how long it will take or if you’ll even succeed, then it will be much harder to convince them to fund you!
Building a model is a totally different skill to checking whether the model has been designed correctly. Apparently.
At one point, I was interviewing for a model validation role. The interviewer didn’t like that I hadn’t done derivative model validation before. It didn’t matter that I had a mathematics PhD, great coding skills and several years experience in derivative modelling. He believed that building mathematical models within a fairly mature derivative pricing system was not the same thing as validating a model from scratch. And, apparently, that skills required for the two roles did not have sufficient overlap.
Shortly thereafter, I got a job doing model validation at a different bank – and of course my general skills and abilities allowed me to perform the role well.
Then a bit later, I heard from a recruiter about a firm that would not consider people working in model validation for a particular role. They held this view because they were looking for someone to “build” models instead of validate them.
For those who don’t know, model validation usually involves building an independent model against which to benchmark the system. It therefore is essentially “building models” anyway.
Then I saw a job advert from Murex which stated that the candidate must have experience developing for Murex 1.3. They were not looking for an experienced quant dev. Or even an experienced dev that was working at the same firm 2 years ago and had a lot of experience developing for Murex 1.29.
By endingly subdividing the industry into more and more specific categories, no candidate is ever quite the right fit for a role.
Mathematics PhDs know less about maths than traders?
I once had an interview for a machine learning role at a prop trading firm. The interviewer was not a mathematician – he was a trader who had at some point studied some machine learning.
“How would you solve a linear regression?”, he asked.
Now, keep in mind that he is talking to someone with a PhD in pure mathematics, who has actually taught 3rd and 4th year mathematics courses at university, and who has several years of postdoctoral research experience. Isn’t it obvious from my background that I don’t need to be assessed on my ability to work with one of the most simple concepts from statistics? I told him that there was an exact formula involving matrices.
“Okay, walk me through that” he persisted.
I told him that I did not recall the formula off the top of my head, but would simply look it up if I needed it.
He next wanted to know if there was anything one needed to do to the data before performing a linear regression. I recalled that the last time I did a linear regression I had to scale the data so that all variables had numbers of a similar order of magnitude.
“Well thaaats interestinggggg! Because it’s scale invariant!”
The trader was probably quite pleased with himself for seemingly tripping me up, and for getting to use a fancy sounded term he had learnt.
I remembered later that the last time I had implemented a linear regression in C++ I had used the gradient descent method. You see, implementing matrix inverses and determinants in C++ is a bit of a pain, and gradient descent converges in only about 5 iterations. It was actually the gradient descent part of the algorithm that required the data scaling. If you solve a linear regression using the matrix formula, you probably don’t need to scale the data. So you see that in a way I was right, but only when solving the regression using the specific method that I had been using. A fact which couldn’t come to light in the short timeframe and pressured questioning of an interview.
“You’ve got machine learning on your CV!”, the trader exclaimed, implying that I clearly knew nothing about machine learning.
As I’ve described already, a mathematics PhD can pick these concepts up very quickly when they need them, but don’t necessarily know them off the tops of their heads. And whether someone has memorised very elementary facts has nothing to do with whether they have the skills to engage in complex research.
There was another trading firm that I interviewed with for what appeared to be a heavily machine learning focused role. I say this because the job description mentioned machine learning not once, but three times. So in the interview, I brought up the topic of machine learning. At first, he didn’t know what I was talking about. Apparently he didn’t know that the job description mentioned machine learning (who wrote the job description, ChatGPT?). Then he said they don’t do machine learning because it overfits. Well, why did they put it in the job description three times then? This is a bit off topic, but it’s so funny I couldn’t resist bringing it up.
Relying on what other people think because you can’t think for yourself
I once had a phone interview with a well-known fund manager in Sydney. I won’t say who he is, other than to say he’s often in the financial news giving his opinions about the economy. He said to me, “If you were paid a lot of money by Westpac, then I’d know you were worth a lot of money!” For those Northern Hemisphere readers, Westpac is an Australian bank that I wasn’t working for at the time of that conversation. The idea was, that if someone else was willing to pay me a lot of money, then he’d believe he should offer me a lot of money. Otherwise he wouldn’t. Relying on the judgement of others to the complete exclusion of your own doesn’t seem wise.
It reminds me of study that found women mainly want to go out with men who already have girlfriends. The authors of the study found women would rate men more attractive if they were told he had a girlfriend, or even if the photo of him showed a random woman smiling in his direction. Apparently, the fact that those men had already been chosen by another girl, convinced other girls that he was worth choosing. Unfortunately, none of those men were available so it seems a poor strategy.
Letting HR design the interview for a role they don’t understand
Years ago, before I started working in quantitative finance, I interviewed with a large Australian telecommunications company called Telstra.
Some manager there had attended a conference where he’d heard about people using statistical methods to model the occurrence of faults in networks, allowing them to move their workers around more efficiently to keep the network operating. Thus, he’d had the idea of hiring a quantitative PhD to do this kind of modelling at Telstra.
What astonished me, is that the interview included not one question about my ability to do statistical modelling. The managers believed that the skills required for statistical modelling didn’t need to be tested and could simply be taken for granted. Indeed, the two managers interviewing me knew little about statistical modelling and simply weren’t qualified to determine whether I was qualified. While I would say that statistical modelling skills were 90% of what was required for the role, these two managers considered them largely irrelevant.
Instead, the interview was a series of HR questions such as, “name a time you’ve worked well on a team”, and “what would you do if you needed someone to do something and they didn’t want to do it”. I remember the female manger kept giggling about she was soon going on holiday to drink cocktails on the beach.
I was entirely unprepared for these sorts of silly questions. Apparently, so were all the other candidates. Indeed, an HR guy from Telstra called me to inform me that they’d decided not to move forward with any of the PhDs they had interviewed because none of them seemed “ready for the role”. While Telstra thought these PhDs could be taught what they were lacking, Telstra was “looking for someone to hit the ground running”.
In the coming years, I kept reading in the news about how Telstra’s network was down again.
Smart people should know everything. Even things you haven’t told them yet!
I’ll end with an Anecdote from the physicist Richard Feynman.
In one of his books, Feynman describes an anecdote from when he was working on the atomic bomb project.
Some engineers presented him with a stack of blueprints representing a proposed chemical facility, and gave him a whirlwind explanation of these very complicated blueprints, leaving him in a daze. He was struggling to guess what the squares with crosses in the middle represented – were they valves or perhaps windows? Since everyone was looking at him, waiting for him to say something, he eventually pointed randomly at one of the squares with crosses in and said, “what happens if this one gets stuck?”
After some frantic whispering, the engineers said “you’re absolutely right, sir”, and rolled up their blueprints and exited the room.
“I knew you were a genius”, the lieutenant said.
Just like in your average job interview, Feynman was being asked to perform a task very quickly, with inadequate information, under pressure. In this case, Feynman got lucky.
Remember, if someone can do something quickly, it’s not because they are a genius – it’s because they’ve done it before.